Advertisements
Advertisements
प्रश्न
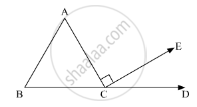
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
उत्तर
In the given figure, AC ⊥ CE and ∠A : ∠B:∠C = 3:2:1. We need to find the value of ∠ECD
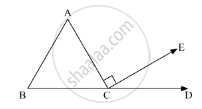
Since,
∠A : ∠B:∠C = 3:2:1
Let,
∠A = 3x
∠B = 2x
∠C = x
Applying the angle sum property of the triangle, in ΔABC, we get,
∠A + ∠B + ∠C = 180°
3x + 2x + x = 180°
6x = 180°
`x = (180°)/6 `
`x = 30°`
Thus,
∠A = 3x = 3(30°) = 90°
∠B = 2x = 2 (30°) = 60°
∠C = x = 30°
Further, BCD is a straight line. So, applying the property, “the angles forming a linear pair are supplementary”, we get,
∠C + ∠ACE + ∠ECD = 180°
∠EDC = 30° + 90° = 180°
∠ECD + 120° = 180°
∠ECD = 180° - 120°
∠ECD = 60°
Therefore, ∠ECD = 60°.
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
Is the following statement true and false :
An exterior angle of a triangle is less than either of its interior opposite angles.
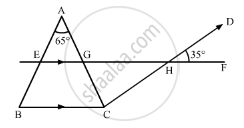
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
Find the unknown marked angles in the given figure:
In the given figure, show that: ∠a = ∠b + ∠c
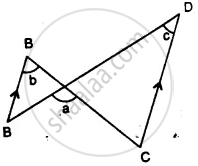
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
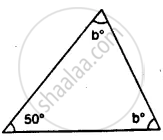
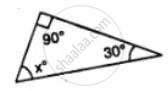
Calculate the unknown marked angles of the following figure :
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
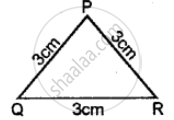
Classify the following triangle according to sides:
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
