Advertisements
Advertisements
प्रश्न
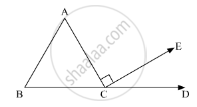
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
उत्तर
In the given figure, AC ⊥ CE and ∠A : ∠B:∠C = 3:2:1. We need to find the value of ∠ECD
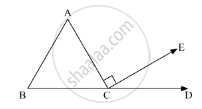
Since,
∠A : ∠B:∠C = 3:2:1
Let,
∠A = 3x
∠B = 2x
∠C = x
Applying the angle sum property of the triangle, in ΔABC, we get,
∠A + ∠B + ∠C = 180°
3x + 2x + x = 180°
6x = 180°
`x = (180°)/6 `
`x = 30°`
Thus,
∠A = 3x = 3(30°) = 90°
∠B = 2x = 2 (30°) = 60°
∠C = x = 30°
Further, BCD is a straight line. So, applying the property, “the angles forming a linear pair are supplementary”, we get,
∠C + ∠ACE + ∠ECD = 180°
∠EDC = 30° + 90° = 180°
∠ECD + 120° = 180°
∠ECD = 180° - 120°
∠ECD = 60°
Therefore, ∠ECD = 60°.
APPEARS IN
संबंधित प्रश्न
If the bisectors of the base angles of a triangle enclose an angle of 135°, prove that the triangle is a right triangle.
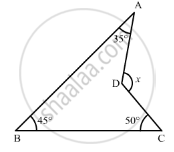
In the given figure, compute the value of x.
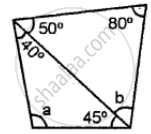
Find the unknown marked angles in the given figure:

In the following, find the marked unknown angle:
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
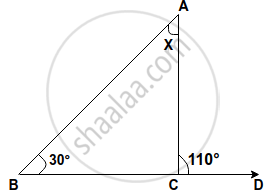
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
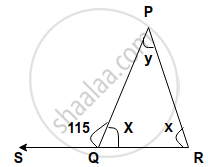
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
7 cm, 24 cm, 25 cm
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
8.4 cm, 16.4 cm, 4.9 cm
The exterior angle of a triangle is equal to the sum of two
Can 30°, 60° and 90° be the angles of a triangle?
