Advertisements
Advertisements
प्रश्न
Compute the value of x in the following figure:
उत्तर
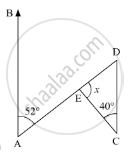
In the given problem, we need to find the value of x
In the given figure, ∠BAD = 52° and ∠DCE = 40°
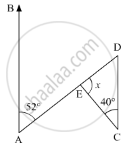
Here,AB || CD and AD is the transversal, so ∠EDC and ∠BAD form a pair of alternate interior angles. Therefore, using the property, “alternate interior angles are equal”, we get,
∠EDC = ∠BAD
∠EDC = 52°
Further, applying angle sum property of the triangle
In ΔDEC
∠DEC + ∠DCE + ∠EDC = 180°
∠DEC + 40° + 52° = 180°
x + 92° = 180°
x = 180° - 92°
x = 88°
Therefore, x = 88°
APPEARS IN
संबंधित प्रश्न
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
Fill in the blank to make the following statement true:
An exterior angle of a triangle is always ......... than either of the interior opposite angles.
Fill in the blank to make the following statement true:
A triangles cannot have more than ......obtuse angles.
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
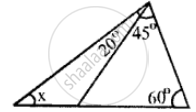
Find the value of the angle in the given figure:

In the following, find the marked unknown angle:
Can a triangle together have the following angles?
85°, 95° and 22°
In the given figure, AB is parallel to CD. Then the value of b is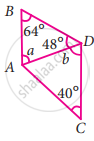
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
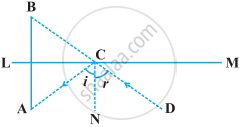
Identify three triangles in the figure.