Advertisements
Advertisements
प्रश्न
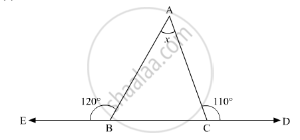
Compute the value of x in the following figure:
उत्तर
In the given problem, we need to find the value of x
In the given ΔABC, ∠ACD = 110° and ∠EBA = 120°
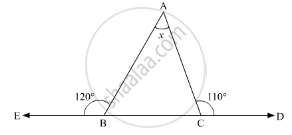
Here, BCD is a straight line. So, using the property, “the angles forming a linear pair are supplementary” we get,
∠ACB + ∠ACD = 180°
∠ACB + 110° = 180°
∠ACB = 180° - 110°
∠ACB = 70°
Similarly, EBC is a straight line. So, we get
∠EBA + ∠ABC = 180°
120° + ∠ABC = 180°
∠ABC = 180° - 120°
∠ABC = 60° V
Further, using the angle sum property of a triangle,
In ΔABC
∠ACB + ∠BAC + ∠ABC = 180°
70° + 60° ∠BAC = 180°
130° + ∠BAC = 180°
∠BAC = 180° - 130°
∠BAC = 50°
Therefore, x = 50°
APPEARS IN
संबंधित प्रश्न
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

Is the following statement true and false :
All the angles of a triangle can be equal to 60°.
State exterior angle theorem.
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
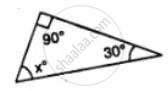
Calculate the unknown marked angles of the following figure :
Find x, if the angles of a triangle is:
x°, x°, x°
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
15 cm, 20 cm, 25 cm
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
