Advertisements
Advertisements
प्रश्न
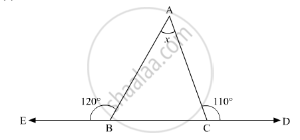
Compute the value of x in the following figure:
Advertisements
उत्तर
In the given problem, we need to find the value of x
In the given ΔABC, ∠ACD = 110° and ∠EBA = 120°
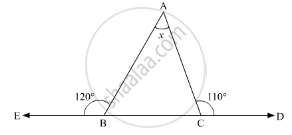
Here, BCD is a straight line. So, using the property, “the angles forming a linear pair are supplementary” we get,
∠ACB + ∠ACD = 180°
∠ACB + 110° = 180°
∠ACB = 180° - 110°
∠ACB = 70°
Similarly, EBC is a straight line. So, we get
∠EBA + ∠ABC = 180°
120° + ∠ABC = 180°
∠ABC = 180° - 120°
∠ABC = 60° V
Further, using the angle sum property of a triangle,
In ΔABC
∠ACB + ∠BAC + ∠ABC = 180°
70° + 60° ∠BAC = 180°
130° + ∠BAC = 180°
∠BAC = 180° - 130°
∠BAC = 50°
Therefore, x = 50°
APPEARS IN
संबंधित प्रश्न
Can a triangle have two right angles? Justify your answer in case.
Fill in the blank to make the following statement true:
A triangle cannot have more than ...... right angles.
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
Calculate the unknown marked angles of the following figure :
Can 30°, 60° and 90° be the angles of a triangle?
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
In ΔABC, name the 
a) Three sides: _________, __________, __________
b) Three Angles: _________, __________, __________
c) Three Vertices: _________, __________, __________
Which two triangles have ∠B in common?
