Advertisements
Advertisements
Question
Compute the value of x in the following figure:
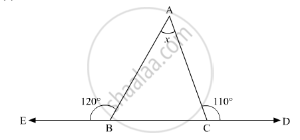
Solution
In the given problem, we need to find the value of x
In the given ΔABC, ∠ACD = 110° and ∠EBA = 120°
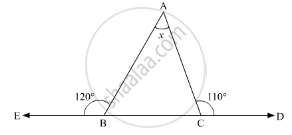
Here, BCD is a straight line. So, using the property, “the angles forming a linear pair are supplementary” we get,
∠ACB + ∠ACD = 180°
∠ACB + 110° = 180°
∠ACB = 180° - 110°
∠ACB = 70°
Similarly, EBC is a straight line. So, we get
∠EBA + ∠ABC = 180°
120° + ∠ABC = 180°
∠ABC = 180° - 120°
∠ABC = 60° V
Further, using the angle sum property of a triangle,
In ΔABC
∠ACB + ∠BAC + ∠ABC = 180°
70° + 60° ∠BAC = 180°
130° + ∠BAC = 180°
∠BAC = 180° - 130°
∠BAC = 50°
Therefore, x = 50°
APPEARS IN
RELATED QUESTIONS
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
Can a triangle have two acute angles?Justify your answer in case.
Can a triangle have All angles more than 60°? Justify your answer in case.
Is the following statement true and false :
An exterior angle of a triangle is less than either of its interior opposite angles.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
Find the unknown marked angles in the given figure:
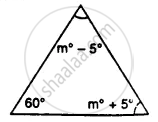
One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
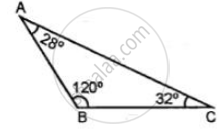
Classify the following triangle according to angle:
The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
