Advertisements
Advertisements
Question
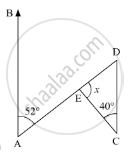
Compute the value of x in the following figure:
Solution
In the given problem, we need to find the value of x
In the given figure, ∠BAD = 52° and ∠DCE = 40°
Here,AB || CD and AD is the transversal, so ∠EDC and ∠BAD form a pair of alternate interior angles. Therefore, using the property, “alternate interior angles are equal”, we get,
∠EDC = ∠BAD
∠EDC = 52°
Further, applying angle sum property of the triangle
In ΔDEC
∠DEC + ∠DCE + ∠EDC = 180°
∠DEC + 40° + 52° = 180°
x + 92° = 180°
x = 180° - 92°
x = 88°
Therefore, x = 88°
APPEARS IN
RELATED QUESTIONS
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
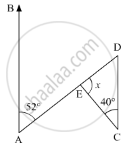
Compute the value of x in the following figure:
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
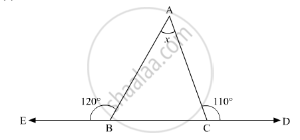
Find the unknown marked angles in the given figure:
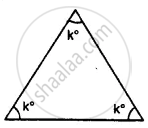
In the following, find the marked unknown angle:

Can a triangle together have the following angles?
85°, 95° and 22°
Find x, if the angles of a triangle is:
2x°, 4x°, 6x°
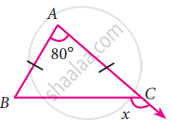
In a ∆ABC, AB = AC. The value of x is ________