Advertisements
Advertisements
Question
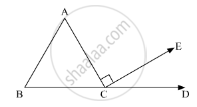
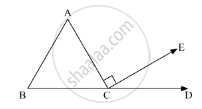
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
Solution
In the given figure, AC ⊥ CE and ∠A : ∠B:∠C = 3:2:1. We need to find the value of ∠ECD
Since,
∠A : ∠B:∠C = 3:2:1
Let,
∠A = 3x
∠B = 2x
∠C = x
Applying the angle sum property of the triangle, in ΔABC, we get,
∠A + ∠B + ∠C = 180°
3x + 2x + x = 180°
6x = 180°
`x = (180°)/6 `
`x = 30°`
Thus,
∠A = 3x = 3(30°) = 90°
∠B = 2x = 2 (30°) = 60°
∠C = x = 30°
Further, BCD is a straight line. So, applying the property, “the angles forming a linear pair are supplementary”, we get,
∠C + ∠ACE + ∠ECD = 180°
∠EDC = 30° + 90° = 180°
∠ECD + 120° = 180°
∠ECD = 180° - 120°
∠ECD = 60°
Therefore, ∠ECD = 60°.
APPEARS IN
RELATED QUESTIONS
In a ΔABC, ∠ABC = ∠ACB and the bisectors of ∠ABC and ∠ACB intersect at O such that ∠BOC = 120°. Show that ∠A = ∠B = ∠C = 60°.
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
Find the unknown marked angles in the given figure:
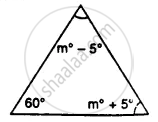
In the following, find the marked unknown angle:

Can a triangle together have the following angles?
33°, 74° and 73°
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Can we have two acute angles whose sum is an acute angle? Why or why not?
Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is point A in its exterior or in its interior?
