Advertisements
Advertisements
Question
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
Options
80°
75°
60°
90°
Solution
In the given problem, side BC of ΔABC has been produced to a point D. Such that ∠ACD = 120° and `∠B = 1/2 ∠A` . Here, we need to find ∠A
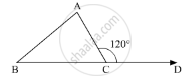
Given `∠B = 1/2 ∠A`
We get, ∠A = 2∠B .........(1)
Now, using the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”, we get,
In ΔABC
∠ACD = ∠A + ∠B
120° = 2∠B + ∠B
120° = 3∠B
`∠B = (120°)/3`
∠B = 40°
Also, ∠A = 2∠B(Using 1)
∠ A = 2 (40°)
= 80°
Thus, ∠A = 80°
APPEARS IN
RELATED QUESTIONS
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
In ΔPQR, If ∠R > ∠Q then ______.
Classify the following triangle according to sides:
The length of the sides of the triangle is given. Say what types of triangles they are 3.4 cm, 3.4 cm, 5 cm.
The length of the sides of the triangle is given. Say what types of triangles they are 3.7 cm, 3.4 cm, 4 cm.
In the given figure, AB is parallel to CD. Then the value of b is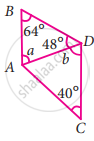
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
