Advertisements
Advertisements
प्रश्न
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
पर्याय
80°
75°
60°
90°
उत्तर
In the given problem, side BC of ΔABC has been produced to a point D. Such that ∠ACD = 120° and `∠B = 1/2 ∠A` . Here, we need to find ∠A
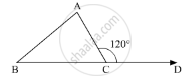
Given `∠B = 1/2 ∠A`
We get, ∠A = 2∠B .........(1)
Now, using the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”, we get,
In ΔABC
∠ACD = ∠A + ∠B
120° = 2∠B + ∠B
120° = 3∠B
`∠B = (120°)/3`
∠B = 40°
Also, ∠A = 2∠B(Using 1)
∠ A = 2 (40°)
= 80°
Thus, ∠A = 80°
APPEARS IN
संबंधित प्रश्न
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

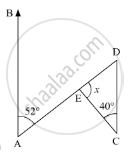
Compute the value of x in the following figure:
Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
Is the following statement true and false :
A triangle can have at most one obtuse angles.
Fill in the blank to make the following statement true:
Sum of the angles of a triangle is ....
In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
