Advertisements
Advertisements
प्रश्न
In Δ ABC, BD⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180° − A.
उत्तर
In the given ΔABC, BD⊥AC and CE⊥AB.
We need prove ∠BOC = 180° - ∠A
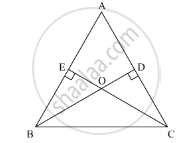
Here, in ΔBDC, using the exterior angle theorem, we get,
∠BDA = ∠DBC + ∠DBC
90 = ∠DBO + ∠DBC ................ (1)
Similarly, in ΔEBC, we get,
∠AEC = ∠EBC + ∠ECB
90 = ∠EBC ∠ECB ................ (2)
Adding (1) and (2), we get,
90 + 90 = ∠DBC + ∠DCB + ∠EBC + ∠ECB
180 = (∠DCB +∠EBC) + (∠DBC+∠ECB)................ (3)
Now, on using angle sum property,
In ΔABC, we get,
∠BAC + ∠ABC + ∠ACB = 180
∠ABC + ∠ACB = 180 - ∠BAC
This can be written as,
∠EBC + ∠DCB = 180 - ∠A ......... (4)
Similarly, using angle sum property in ΔOBC, we get,
∠BOC + ∠OBC + ∠OCB = 180
∠OBC + ∠OCB = 180 - ∠BOC
This can be written as,
∠DBC + ∠ECB = 180 - ∠BOC ......... (5)
Now, using the values of (4) and (5) in (3), we get,
180 = 180 - ∠BOC ........... (5)
180 = 360 - ∠A - ∠BOC
∠BOC = 360 - 180 - ∠A
∠BOC = 180 - ∠A
Therefore, ∠BOC = 180 - ∠A.
Hence proved
APPEARS IN
संबंधित प्रश्न
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
Classify the following triangle according to sides:
The exterior angle of a triangle is equal to the sum of two
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
In figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is ______.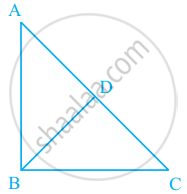
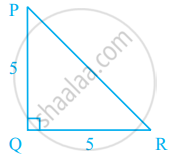
In figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆PQR is ______.