Advertisements
Advertisements
प्रश्न
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
उत्तर
In Δ ABC,
Let ∠A = 60° and then ∠B: ∠C = 5: 7
But ∠A + ∠B + ∠C = 180° ........(Angles of a triangle)
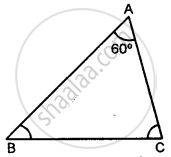
⇒ 60° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180°− 60° = 120°
Let ∠B = 5x and ∠C = 7x
∴ 5x + 7x = 120°
⇒ 12x = 120°
⇒ x =`(120°)/12=10°`
∴ ∠B = 5x = 5 × 10° = 50°
∠C = 7x = 7 × 10° = 70°
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
ABC is a triangle in which ∠A — 72°, the internal bisectors of angles B and C meet in O.
Find the magnitude of ∠BOC.
Can a triangle have All angles equal to 60°? Justify your answer in case.
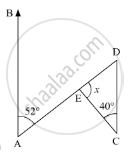
Compute the value of x in the following figure:
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
Find, giving a reason, the unknown marked angles, in a triangle drawn below:

The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
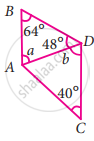
In the given figure, AB is parallel to CD. Then the value of b is