Advertisements
Advertisements
प्रश्न
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
उत्तर
We know that the sum of three angles of a triangle is 180°, therefore
Sum of 125°, 40°, and 15°
= 125° + 40° + 15° = 180°
Since the sum is 180°, therefore it is possible.
APPEARS IN
संबंधित प्रश्न
Can a triangle have two right angles? Justify your answer in case.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
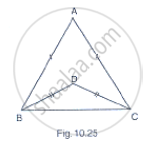
In Fig. 10.25, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
Can a triangle together have the following angles?
33°, 74° and 73°
Can a triangle together have the following angles?
85°, 95° and 22°
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
Identify three triangles in the figure.