Advertisements
Advertisements
प्रश्न
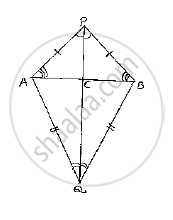
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

उत्तर
Consider the figure,
We have
AB is a line segment and P,Q are points on opposite sides of AB such that
AP= BP .........................(1)
AQ= BQ ........................(2)
We have to prove that PQ is perpendicular bisector of AB.
Now consider ΔPAQand ΔPBQ,
We have AP = BP [∵ from (1)]
AQ = BQ [∵ from (2)]
And PQ = PQ [Common site]
ΔPAQ ≅ ΔPBQ .......................(3) [From SSS congruence]
Now, we can observe that Δ𝐴𝑃𝐵 𝑎𝑛𝑑 Δ𝐴𝐵𝑄 are isosceles triangles.(From 1 and 2)
⇒ ∠𝑃𝐴𝐵 = ∠𝑃𝐵𝐴 𝑎𝑛𝑑 ∠𝑄𝐴𝐵 = ∠𝑄𝐵𝐴
Now consider Δ PAC and , ΔPBC
C is the point of intersection of AB and PQ.
PA= PB [From (1)]
∠APC=∠BPC [From (3)]
PC= PC [Common side]
So, from SAS congruency of triangle Δ PAC≅ Δ PBC
⇒ AC = CB and∠PCA = ∠PCB …….(4)
[ ∵Corresponding parts of congruent triangles are equal]
And also, ACB is line segment
⇒∠ACP +∠BCP =180°
But∠ ACP=PCB
∠ACP =∠PCB =90° .........................(5)
We have AC = CBWe have AC = CB C We have AC = CB ⇒ is the midpoint of AB
From (4) and (5)
We can conclude that PC is the perpendicular bisector of AB
Since C is a point on the line PQ, we can say that PQ is the perpendicular bisector of AB.