Question

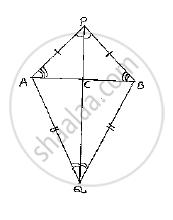
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB. 

 

Answer 1

Consider the figure,
We have
AB is a line segment and P,Q are points on opposite sides of AB such that  

AP= BP                   .........................(1) 
AQ= BQ                   ........................(2) 

We have to prove that PQ is perpendicular bisector of AB.
Now consider ΔPAQand ΔPBQ, 

We have AP = BP               [∵ from (1)]

AQ = BQ                            [∵ from (2)] 

And PQ = PQ                    [Common site] 

ΔPAQ ≅ ΔPBQ             .......................(3)              [From SSS congruence] 

Now, we can observe that Δ𝐴𝑃𝐵 𝑎𝑛𝑑 Δ𝐴𝐵𝑄 are isosceles triangles.(From 1 and 2) 

⇒ ∠𝑃𝐴𝐵 = ∠𝑃𝐵𝐴 𝑎𝑛𝑑 ∠𝑄𝐴𝐵 = ∠𝑄𝐵𝐴 

Now consider Δ PAC and , ΔPBC
C is the point of intersection of AB and PQ.  

PA= PB                       [From (1)]  

∠APC=∠BPC              [From (3)] 

PC= PC                    [Common side]  

So, from SAS congruency of triangle Δ PAC≅ Δ PBC 

⇒ AC = CB and∠PCA = ∠PCB …….(4) 

[ ∵Corresponding parts of congruent triangles are equal]
And also, ACB is line segment  

⇒∠ACP +∠BCP =180° 

But∠ ACP=PCB 

∠ACP =∠PCB =90°                     .........................(5) 

We have AC = CBWe have AC = CB C We have AC = CB ⇒ is the midpoint of AB  
From (4) and (5)

We can conclude that PC is the perpendicular bisector of AB
Since C is a point on the line PQ, we can say that PQ is the perpendicular bisector of AB.