Advertisements
Advertisements
प्रश्न
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
उत्तर
We know that the sum of three angles of a triangle is 180°, therefore
Sum of 125°, 40°, and 15°
= 125° + 40° + 15° = 180°
Since the sum is 180°, therefore it is possible.
APPEARS IN
संबंधित प्रश्न
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
Is the following statement true and false :
If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
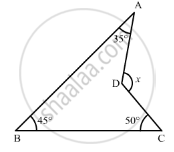
In the given figure, compute the value of x.
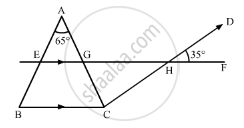
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
Calculate the unknown marked angles of the following figure :
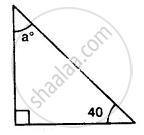
Find x, if the angles of a triangle is:
2x°, 4x°, 6x°
Classify the following triangle according to angle:
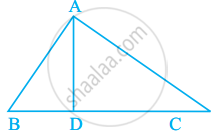
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.