Advertisements
Advertisements
प्रश्न
Is the following statement true and false :
If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
विकल्प
Ture
False
उत्तर
If one angle of a triangle is obtuse, then it cannot be a right angles triangle.
According to the angle sum property of the triangle
In ΔABC
∠A +∠B + ∠C = 180°
Now, if it is a right angled triangle
Then,
∠A + ∠B + ∠C = 180°
90° + ∠B + ∠C =180°
∠B +∠C = 90°
Also if one of the angle’s is obtuse
∠B +∠C > 90°
This is not possible.
Thus, if one angle of a triangle is obtuse, then it cannot be a right angled triangle.
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
A triangle can have two right angles.
Is the following statement true and false :
All the angles of a triangle can be greater than 60°.
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
One angle of a right-angled triangle is 70°. Find the other acute angle.
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
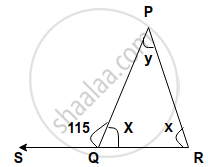
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
