Advertisements
Advertisements
प्रश्न
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
उत्तर
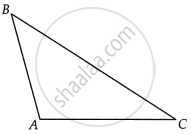
Consider: ΔABC in which BC is the longest side.
To prove: ∠A = `2/3` right angle
Proof: In ΔABC, BC > AB ...[Consider BC is the largest side]
⇒ ∠A > ∠C ...(i) [Angle opposite the longest side is greatest]
And BC > AC
⇒ ∠A > ∠B ...(ii) [Angle opposite the longest side is greatest]
On adding equation (i) and (ii), we get
2∠A > ∠B + ∠C
⇒ 2∠A + ∠A > ∠A + ∠B + ∠C ...[Adding ∠A both sides]
⇒ 3∠A > ∠A + ∠B + ∠C
⇒ 3∠A > 180° ...[Sum of all the angles of a triangle is 180°]
⇒ ∠A > `2/3 xx 90^circ`
i.e., ∠A > `2/3` of a right angle
Hence proved.
APPEARS IN
संबंधित प्रश्न
Fill in the blank to make the following statement true:
A triangle cannot have more than ...... right angles.
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
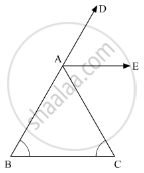
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
Find the value of the angle in the given figure:
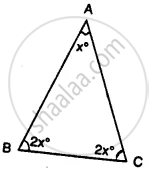
Find the unknown marked angles in the given figure:
Can a triangle together have the following angles?
33°, 74° and 73°
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
9 cm, 6 cm, 16 cm
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.