Advertisements
Advertisements
प्रश्न
ABCD is quadrilateral such that AB = AD and CB = CD. Prove that AC is the perpendicular bisector of BD.
उत्तर
Given: In quadrilateral ABCD, AB = AD and CB = CD.
Construction: Join AC and BD.
To prove: AC is the perpendicular bisector of BD.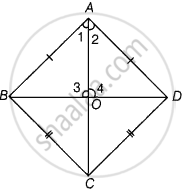
Proof: In ΔABC and ΔADC,
AB = AD ...[Given]
BC = CD ...[Given]
And AC = AC ...[Common side]
∴ ΔABC ≅ ΔADC ...[By SSS congruence rule]
⇒ ∠1 = ∠2 ...[By CPCT]
Now, in ΔAOB and ΔAOD,
AB = AD ...[Given]
⇒ ∠1 = ∠2 ...[Proved above]
And AO = AO ...[Common side]
∴ ΔAOB ≅ ΔAOD ...[By SAS congruence rule]
⇒ BO = DO ...[Bt CPCT]
And ∠3 = ∠4 [By CPCT] ...(i)
But ∠3 + ∠4 = 180° ...[Linear pair axiom]
∠3 + ∠3 = 180° ...[From equation (i)]
⇒ 2∠3 = 180°
⇒ ∠3 = `(180^circ)/2`
∴ ∠3 = 90°
i.e., AC is perpendicular bisector of BD.
APPEARS IN
संबंधित प्रश्न
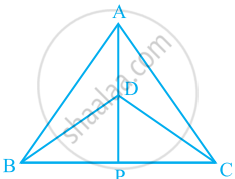
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that
- ΔABD ≅ ΔACD
- ΔABP ≅ ΔACP
- AP bisects ∠A as well as ∠D.
- AP is the perpendicular bisector of BC.
AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that
- AD bisects BC
- AD bisects ∠A
ABC is an isosceles triangle with AB = AC. Drawn AP ⊥ BC to show that ∠B = ∠C.
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the other. Prove that the triangles are congruent.
Prove that in a quadrilateral the sum of all the sides is greater than the sum of its diagonals.
In the following figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that ∆ABC ≅ ∆DEF.
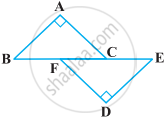
ABC is an isosceles triangle in which AC = BC. AD and BE are respectively two altitudes to sides BC and AC. Prove that AE = BD.
Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.
Two lines l and m intersect at the point O and P is a point on a line n passing through the point O such that P is equidistant from l and m. Prove that n is the bisector of the angle formed by l and m.
ABC is a right triangle such that AB = AC and bisector of angle C intersects the side AB at D. Prove that AC + AD = BC.
