Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle in which AC = BC. AD and BE are respectively two altitudes to sides BC and AC. Prove that AE = BD.
उत्तर
Given: ΔABC is an isosceles triangle in which AC = BC.
Also, AD and BE are two altitudes to sides BC and AC, respectively.
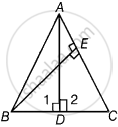
To prove: AE = BD
Proof: In ΔABC,
AC = BC ...[Given]
∠ABC = ∠CAB ...[Angles opposite to equal sides are equal]
i.e., ∠ABD = ∠EAB ...(i)
In ΔAEB and ΔBDA,
∠AEB = ∠ADB = 90° ...[Given, AD ⊥ BC and BE ⊥ AC]
∠EAB = ∠ABD ...[From equation (i)]
And AB = AB ...[Common side]
∴ ΔAEB ≅ ΔBDA ...[By AAS congruence rule]
⇒ AE = BD ...[By CPCT]
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
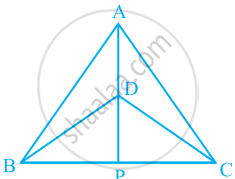
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see the given figure). If AD is extended to intersect BC at P, show that
- ΔABD ≅ ΔACD
- ΔABP ≅ ΔACP
- AP bisects ∠A as well as ∠D.
- AP is the perpendicular bisector of BC.
AD is an altitude of an isosceles triangles ABC in which AB = AC. Show that
- AD bisects BC
- AD bisects ∠A
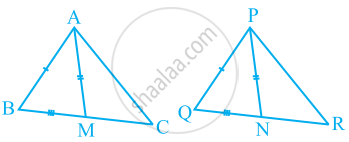
Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see the given figure). Show that:
- ΔABM ≅ ΔPQN
- ΔABC ≅ ΔPQR
ABC is an isosceles triangle with AB = AC. Drawn AP ⊥ BC to show that ∠B = ∠C.
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the other. Prove that the triangles are congruent.
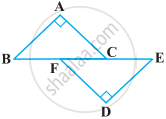
In the following figure, BA ⊥ AC, DE ⊥ DF such that BA = DE and BF = EC. Show that ∆ABC ≅ ∆DEF.
ABC and DBC are two triangles on the same base BC such that A and D lie on the opposite sides of BC, AB = AC and DB = DC. Show that AD is the perpendicular bisector of BC.
In a right triangle, prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.
Two lines l and m intersect at the point O and P is a point on a line n passing through the point O such that P is equidistant from l and m. Prove that n is the bisector of the angle formed by l and m.
