Advertisements
Advertisements
प्रश्न
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
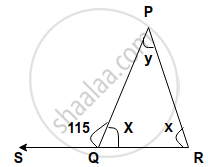
उत्तर
We know that,
Exterior angle of a triangle is always equal to the sum of its two interior opposite angles (property)
x+115° = 180°
(linear property of angles)
⇒ x = 180°- 115° ⇒ x = 65°
∴115° = x + y
⇒ 115° = 65° + y
⇒ y= 115° – 65° =50°
y = 50°
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
Is the following statement true and false :
A triangle can have at most one obtuse angles.
Is the following statement true and false :
If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
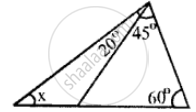
In the following, find the marked unknown angle:
Find x, if the angles of a triangle is:
x°, x°, x°
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
Can we have two acute angles whose sum is an acute angle? Why or why not?
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
