Advertisements
Advertisements
प्रश्न
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
उत्तर
In the given problem, we need to find the difference between the sum of the exterior angles and∠A.
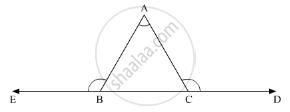
Now, according to the exterior angle theorem
ext. ∠C = ∠A + ∠B .........(1)
Also,
ext. ∠B = ∠A + ∠C .........(2)
Further, adding (1) and (2)
ext. ∠C + ext. ∠B = ∠A + ∠B + ∠A + ∠B
=2∠A+ ∠B + ∠C .........(3)
Also, according to the angle sum property of the triangle, we get,
∠A + ∠B + ∠C = 180° .........(4)
Now, we need to find the difference between the sum of the exterior angles and ∠A
Thus,
( ext. ∠C + ext. ∠B) - ∠A = (2∠A + ∠B + ∠C ) - ∠A
= ∠A = ∠B + ∠C
= 180°(Using 4)
Therefore, (ext. ∠C ext.∠B) -∠A = 180°
APPEARS IN
संबंधित प्रश्न
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
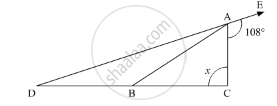
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
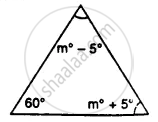
Find the value of the angle in the given figure:

Find the unknown marked angles in the given figure:
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
S is any point on side QR of a ∆PQR. Show that: PQ + QR + RP > 2PS.
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
