Advertisements
Advertisements
प्रश्न
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
उत्तर
In a ABC
Sum of all angles of triangles is `180^@`
i.e, `∠ A+∠ B+∠C =180^@` divide both sides by `2`
⇒ `1/2∠A+1/2∠B+1/2∠C=180^@`
⇒`1/2∠A+∠OBC+∠OBC=90^@` [∵ OB,OC insects ∠B and ∠C]
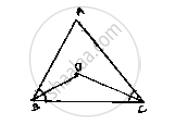
⇒`∠OBC+∠OCB=90^@-1/2A`
Now in `Δ OCB=180^@`
`∴ ∠ BOC+∠OBC+∠OCB=180^@`
⇒`∠ BOC+90^@-1/2∠A=180^@`
⇒ `∠ BOC=90^@-1/2 ∠A`
Hence, bisectors of a base angle cannot enclose right angle.
APPEARS IN
संबंधित प्रश्न
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
Can a triangle have All angles less than 60° Justify your answer in case.
Compute the value of x in the following figure:
State exterior angle theorem.
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
Find the value of the angle in the given figure:

Find x, if the angles of a triangle is:
x°, 2x°, 2x°
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.