Advertisements
Advertisements
Question
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Solution
In a ABC
Sum of all angles of triangles is `180^@`
i.e, `∠ A+∠ B+∠C =180^@` divide both sides by `2`
⇒ `1/2∠A+1/2∠B+1/2∠C=180^@`
⇒`1/2∠A+∠OBC+∠OBC=90^@` [∵ OB,OC insects ∠B and ∠C]
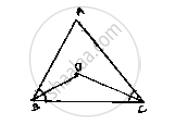
⇒`∠OBC+∠OCB=90^@-1/2A`
Now in `Δ OCB=180^@`
`∴ ∠ BOC+∠OBC+∠OCB=180^@`
⇒`∠ BOC+90^@-1/2∠A=180^@`
⇒ `∠ BOC=90^@-1/2 ∠A`
Hence, bisectors of a base angle cannot enclose right angle.
APPEARS IN
RELATED QUESTIONS
Is the following statement true and false :
All the angles of a triangle can be equal to 60°.
Is the following statement true and false :
A triangle can have two obtuse angles.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
In ΔPQR, If ∠R > ∠Q then ______.
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
The length of the sides of the triangle is given. Say what types of triangles they are 3.7 cm, 3.4 cm, 4 cm.
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.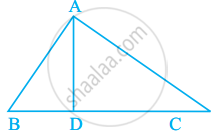
In figure, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.