Advertisements
Advertisements
Question
If the bisectors of the base angles of a triangle enclose an angle of 135°, prove that the triangle is a right triangle.
Solution
Given the bisectors the base angles of an triangle enclose an angle of `135^@`
i.e., ∠BOC=`135^@`
But, W.K.T
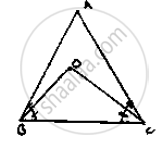
`∠ BOC=90^@+1/2∠B`
⇒ `135^@=90^@+1/2∠A`
⇒`1/2∠A=135^@-90^@`
⇒`∠A=45^@(2)`
⇒`∠A=90^@`
∴ ΔABC is right angled triangle right angled at A.
APPEARS IN
RELATED QUESTIONS
Can a triangle have two acute angles?Justify your answer in case.
Fill in the blank to make the following statement true:
A triangle cannot have more than ...... right angles.
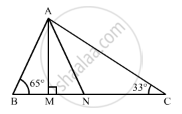
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
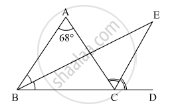
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
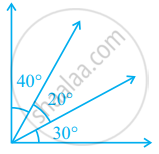
Find the unknown marked angles in the given figure:
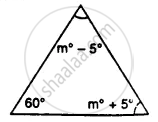
Classify the following triangle according to angle:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
15 cm, 20 cm, 25 cm
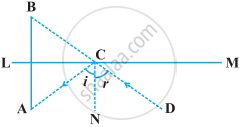
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
The number of angles in figure is ______.