Advertisements
Advertisements
Question
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
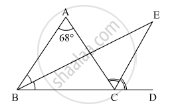
Solution
In the given figure, bisectors of ∠ABC and ∠ACD meet at E and ∠BAC = 68°
We need to find ∠BEC
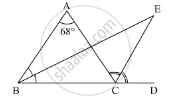
Here, using the property: an exterior angle of the triangle is equal to the sum of the opposite interior angles.
In ΔABC with ∠ACD as its exterior angle
exterior ∠ACD = ∠A +∠ABC ........(1)
Similarly, in ΔBE with ∠ECD as its exterior angle
exterior ∠ECD = ∠EBC + ∠BEC
`1/2 ∠"ACD" = 1/2 ∠"ABC" + ∠"BEC"` (CE and BE are the bisectors of ∠ACD and) ∠ABC
`∠"BEC" = 1/2 ∠"ACD" - 1/2 ∠"ABC"` ........(2)
Now, multiplying both sides of (1) by 1/2
We get,
`1/2 ∠"ACD" = 1/2 ∠"A" +1/2 ∠"ABC"`
`1/2 ∠"A" = 1/2 ∠"ACD" - 1/2∠"ABC"` ........(3)
From (2) and (3) we get,
`∠"BEC" = 1/2 ∠"A"`
`∠"BEC" = 1/2(68°)`
∠BEC = 34°
Thus, ∠BEC = 34°
APPEARS IN
RELATED QUESTIONS
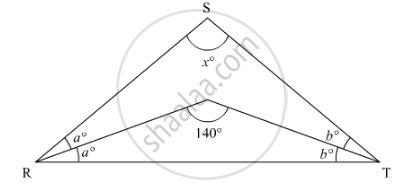
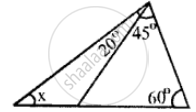
In ΔRST (See figure), what is the value of x?
If two sides of a triangle are 5 cm and 1.5 cm, the length of its third side cannot be ______.
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
In the following, find the marked unknown angle:
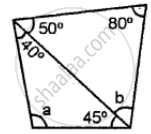
In the following, find the marked unknown angle:
The length of the sides of the triangle is given. Say what types of triangles they are 3.7 cm, 3.4 cm, 4 cm.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
17 cm, 7 cm, 8 cm
The correct statement out of the following is 
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
