Advertisements
Advertisements
Question
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
Solution
Given in the question, P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q.
To prove: BPQ is an isosceles triangle.
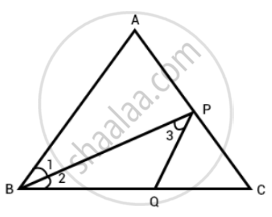
Proof: ∠1 = ∠2 ...(i) [BP is the bisector of ∠ABC]
PQ is parallel to BA and BP cuts them.
So, ∠1 = ∠3 ...[Alternate interior angles as PQ || AB]
∠2 = ∠3 ...[Proved above]
PQ = BQ ...[Sides opposite to equal angle are equal]
Hence, BPQ is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
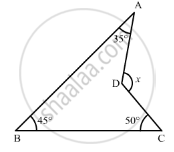
In the given figure, compute the value of x.
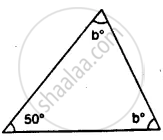
Find the unknown marked angles in the given figure:
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
One of the base angles of an isosceles triangle is 52°. Find its angle of the vertex.
In the following, find the marked unknown angle:

One angle of a right-angled triangle is 70°. Find the other acute angle.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
8.4 cm, 16.4 cm, 4.9 cm
Can 30°, 60° and 90° be the angles of a triangle?
AB and CD are the smallest and largest sides of a quadrilateral ABCD. Out of ∠B and ∠D decide which is greater.
Can we have two acute angles whose sum is a straight angle? Why or why not?
