Advertisements
Advertisements
Question
In the given figure, compute the value of x.
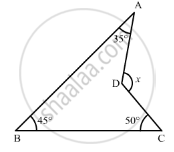
Solution
In the given figure,∠DCB = 45, ∠CBA = 45 and ∠BAD = 35
Here, we will produce AD to meet BC at E

Now, using angle sum property of the triangle
In ΔAEB
∠BAE +∠AEB + ∠EBA = 180°
∠AED + 35°+ 45° = 180°
∠AEB + 80° = 180°
∠AEB = 180° - 80°
∠AEB = 100°
Further, BEC is a straight line. So, using the property, “the angles forming a linear pair are supplementary”, we get,
∠AEB + ∠AEC = 180°
100 + ∠AEC = 180°
∠AEC = 180°- 100°
∠AEC = 80°
Also, using the property, “an exterior angle of a triangle is equal to the sum of its two opposite interior angles”
In ΔDEC, x is its exterior angle
Thus,
∠X = ∠DCE + ∠DEC
= 50° + 80°
= 130°
Therefore, X = 130°.
APPEARS IN
RELATED QUESTIONS
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
Can a triangle have two obtuse angles? Justify your answer in case.
Can a triangle have All angles more than 60°? Justify your answer in case.
Can a triangle have All angles less than 60° Justify your answer in case.
Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
Is the following statement true and false :
All the angles of a triangle can be less than 60°
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
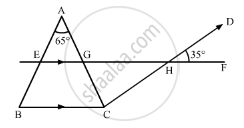
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
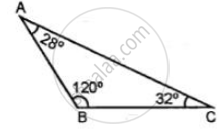
Classify the following triangle according to angle:
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
