Advertisements
Advertisements
Question
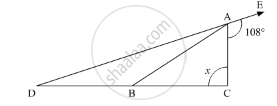
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
Solution
In the given figure,∠EAC = 108° and DB = AB

Since,DB = AB and angles opposite to equal sides are equal. We get,
\[\angle BDA = \angle BAD . . . . . \left( 1 \right)\]
Also, EAD is a straight line. So, using the property, “the angles forming a linear pair are supplementary”, we get,
∠EAC + ∠DAC =- 180°
∠DAC + 180° = 180°
∠DAC = 180° - 108°
∠DAC = 72°
Further, it is given AB divides ∠DAC in the ratio 1 : 3.
So, let
\[\angle DAB = y, \angle BAC = 3y\]
Thus,
\[y + 3y = \angle DAC\]
\[ \Rightarrow 4y = 72^\circ \]
\[ \Rightarrow y = \frac{72^\circ}{4}\]
\[ \Rightarrow y = 18^\circ\]
Hence.
\[\angle DAB = 18^\circ, \angle BAC = 3 \times 18^\circ = 54^\circ\]
Using (1)
∠BDA = ∠DAB
∠BDA = 18°
Now, in ΔABC , using the property, “exterior angle of a triangle is equal to the sum of its two opposite interior angles”, we get,
\[\angle EAC = \angle ADC + x\]
\[ \Rightarrow 108^\circ = 18^\circ + x\]
\[ \Rightarrow x = 90^\circ\]
APPEARS IN
RELATED QUESTIONS
In a ΔABC, if ∠A = 55°, ∠B = 40°, find ∠C.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
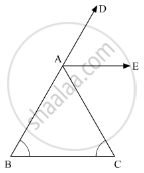
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
The angle of a vertex of an isosceles triangle is 100°. Find its base angles.
Classify the following triangle according to sides:
The correct statement out of the following is 
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
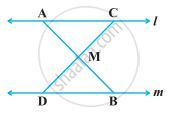
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.