Advertisements
Advertisements
प्रश्न
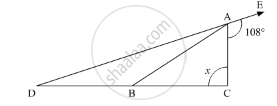
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
उत्तर
In the given figure,∠EAC = 108° and DB = AB

Since,DB = AB and angles opposite to equal sides are equal. We get,
\[\angle BDA = \angle BAD . . . . . \left( 1 \right)\]
Also, EAD is a straight line. So, using the property, “the angles forming a linear pair are supplementary”, we get,
∠EAC + ∠DAC =- 180°
∠DAC + 180° = 180°
∠DAC = 180° - 108°
∠DAC = 72°
Further, it is given AB divides ∠DAC in the ratio 1 : 3.
So, let
\[\angle DAB = y, \angle BAC = 3y\]
Thus,
\[y + 3y = \angle DAC\]
\[ \Rightarrow 4y = 72^\circ \]
\[ \Rightarrow y = \frac{72^\circ}{4}\]
\[ \Rightarrow y = 18^\circ\]
Hence.
\[\angle DAB = 18^\circ, \angle BAC = 3 \times 18^\circ = 54^\circ\]
Using (1)
∠BDA = ∠DAB
∠BDA = 18°
Now, in ΔABC , using the property, “exterior angle of a triangle is equal to the sum of its two opposite interior angles”, we get,
\[\angle EAC = \angle ADC + x\]
\[ \Rightarrow 108^\circ = 18^\circ + x\]
\[ \Rightarrow x = 90^\circ\]
APPEARS IN
संबंधित प्रश्न
Can a triangle have two right angles? Justify your answer in case.
Can a triangle have two acute angles?Justify your answer in case.
Can a triangle have All angles more than 60°? Justify your answer in case.
In the given figure, AB || DE. Find ∠ACD.

The sum of two angles of a triangle is equal to its third angle. Determine the measure of the third angle.
In ΔABC, if bisectors of ∠ABC and ∠ACB intersect at O at angle of 120°, then find the measure of ∠A.
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
In the given figure, show that: ∠a = ∠b + ∠c
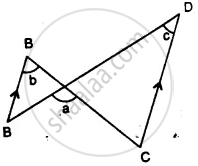
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
15 cm, 20 cm, 25 cm
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
