Advertisements
Advertisements
प्रश्न
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
विकल्प
48°, 60°, 72°
50°, 60°, 70°
52°, 56°, 72°
42°, 60°, 76°
उत्तर
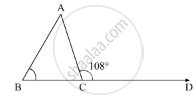
In the given ΔABC, an exterior angle ∠ADC = 108° and its interior opposite angles are in the ratio 4:5.
Let us take,
∠A = 4x
∠B = 5x
Now using the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”
We get,
∠A + ∠B = 108°
4x + 5x = 108°
9x = 108°
`x = (108°)/ 9`
x = 12
Thus,
∠A = 4x = 4(12°) = 48°
∠B = 5x = 5(12°) = 60°
Also, using angle sum property in ΔABC
∠A + ∠B + ∠C = 180°
48° + 60° + ∠C = 180°
108° + ∠C = 180°
∠C = 180° - 108°
∠C = 72°
Thus,
∠A = 48°
∠B = 60°
∠C = 72°
APPEARS IN
संबंधित प्रश्न
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

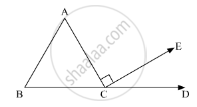
In the given figure, AC ⊥ CE and ∠A : ∠B : ∠C = 3 : 2 : 1, find the value of ∠ECD.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
In a triangle, an exterior angle at a vertex is 95° and its one of the interior opposite angle is 55°, then the measure of the other interior angle is
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
15 cm, 20 cm, 25 cm
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
12 cm, 12 cm, 16 cm
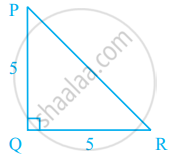
In figure, PQ ⊥ RQ, PQ = 5 cm and QR = 5 cm. Then ∆PQR is ______.