Advertisements
Advertisements
Question
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
Options
48°, 60°, 72°
50°, 60°, 70°
52°, 56°, 72°
42°, 60°, 76°
Solution
In the given ΔABC, an exterior angle ∠ADC = 108° and its interior opposite angles are in the ratio 4:5.
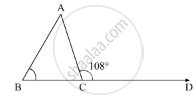
Let us take,
∠A = 4x
∠B = 5x
Now using the property, “exterior angle of a triangle is equal to the sum of two opposite interior angles”
We get,
∠A + ∠B = 108°
4x + 5x = 108°
9x = 108°
`x = (108°)/ 9`
x = 12
Thus,
∠A = 4x = 4(12°) = 48°
∠B = 5x = 5(12°) = 60°
Also, using angle sum property in ΔABC
∠A + ∠B + ∠C = 180°
48° + 60° + ∠C = 180°
108° + ∠C = 180°
∠C = 180° - 108°
∠C = 72°
Thus,
∠A = 48°
∠B = 60°
∠C = 72°
APPEARS IN
RELATED QUESTIONS
If one angle of a triangle is equal to the sum of the other two, show that the triangle is a
right triangle.
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
In the given figure, show that: ∠a = ∠b + ∠c
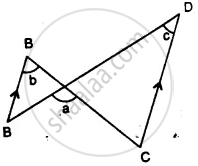
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
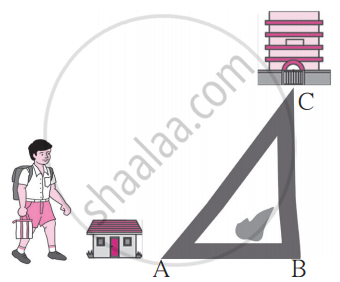
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
Q is a point on the side SR of a ∆PSR such that PQ = PR. Prove that PS > PQ.
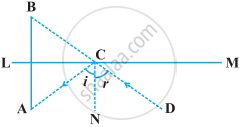
The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D as shown in the following figure. Prove that the image is as far behind the mirror as the object is in front of the mirror.
[Hint: CN is normal to the mirror. Also, angle of incidence = angle of reflection].
The number of triangles in figure is ______.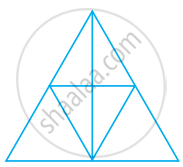
Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is point A in its exterior or in its interior?
