Advertisements
Advertisements
Question
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
Options
75°
80°
80°
40°
50°
Solution
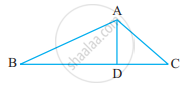
n the ΔABC, CD is the ray extended from the vertex C of ΔABC. It is given that the exterior angle of the triangle is 100° and two of the interior opposite angles are equal.
So, ∠ACD = 100° and A = ∠B
So, now using the property, “an exterior angle of the triangle is equal to the sum of the two opposite interior angles”, we get.
In ΔABC
∠A + ∠B = ∠ACD
∠2A = 100°
`∠A = (100°)/2`
∠A = 50°
∠A = ∠B = 50°
Therefore, each of the two opposite interior angles is 50°.
APPEARS IN
RELATED QUESTIONS
Determine the measure of each of the equal angles of a right-angled isosceles triangle.
OR
ABC is a right-angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.
Is the following statement true and false :
A triangle can have at most one obtuse angles.
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
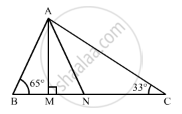
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
Mark the correct alternative in each of the following:
If all the three angles of a triangle are equal, then each one of them is equal to
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Find, giving a reason, the unknown marked angles, in a triangle drawn below:

The length of the sides of the triangle is given. Say what types of triangles they are 3.4 cm, 3.4 cm, 5 cm.
The number of triangles in figure is ______.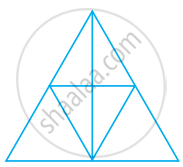
Identify three triangles in the figure.