Advertisements
Advertisements
Question
If two acute angles of a right triangle are equal, then each acute is equal to
Options
30°
45°
60°
90°
Solution
In the given problem, we have a right angled triangle and the other two angles are equal.
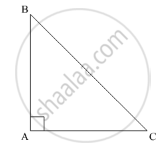
So, In ΔABC
∠A = 90°
∠B = ∠C
Now, using the angle sum property of the triangle, in ΔABC, we get,
∠A + ∠B + ∠C = 180°
90° + 2∠B = 180° (∠B = ∠C)
2∠B= 180° - 90°
`∠B = (90°)/2`
∠B = 45°
APPEARS IN
RELATED QUESTIONS
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
If the bisectors of the base angles of a triangle enclose an angle of 135°, prove that the triangle is a right triangle.
Is the following statement true and false :
A triangle can have two right angles.
Is the following statement true and false :
All the angles of a triangle can be greater than 60°.
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
In ΔPQR, If ∠R > ∠Q then ______.
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
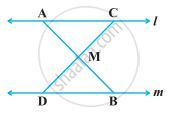
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
