Advertisements
Advertisements
Question
Is the following statement true and false :
A triangle can have at most one obtuse angles.
Options
Ture
False
Solution
A triangle can have at most one obtuse angle.
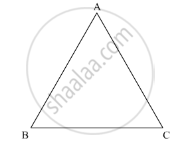
According to the angle sum property of the triangle
In ΔABC
∠A + ∠B + ∠C = 180°
Now, if a triangle will have more than one obtuse angle
Then,
∠A + ∠B + ∠C > 180°
APPEARS IN
RELATED QUESTIONS
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
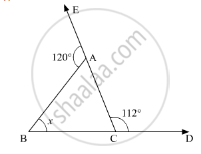
Compute the value of x in the following figure:
Fill in the blank to make the following statement true:
A triangles cannot have more than ......obtuse angles.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
In ΔPQR, If ∠R > ∠Q then ______.
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
Can you draw a triangle with 25°, 65° and 80° as angles?
In a ∆ABC, AB = AC. The value of x is ________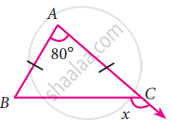
What is common in the following figure?
 |
 |
| (i) | (ii) |
Is figure (i) that of triangle? if not, why?
