Advertisements
Advertisements
Question
Fill in the blank to make the following statement true:
A triangles cannot have more than ......obtuse angles.
Solution
A triangle cannot have more than one obtuse angle
As the sum of all the angles of a triangle is 180°. So, if the triangle has more than one obtuse angle the sum would exceed 180°.
APPEARS IN
RELATED QUESTIONS
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
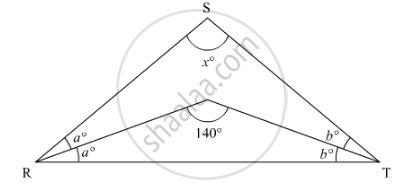
In ΔRST (See figure), what is the value of x?
State, if the triangle is possible with the following angles :
125°, 40°, and 15°
If the angles of a triangle are equal, find its angles.
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
D is any point on side AC of a ∆ABC with AB = AC. Show that CD < BD.
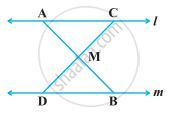
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
In figure, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.