Advertisements
Advertisements
Question
In ΔRST (See figure), what is the value of x?
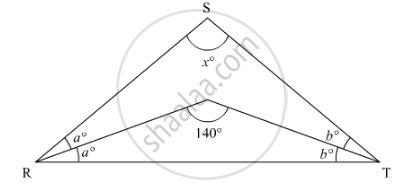
Options
40°
90°
80°
100°
Solution
In the given problem, we need to find the value of x.
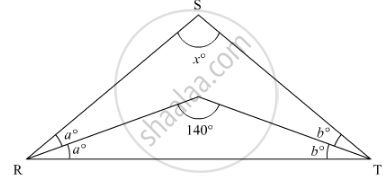
Here, according to the corollary, “if bisectors of ∠ABC and ∠ACBof a ΔABC meet at a point O, then ∠BOC = 90° + 1/2 ∠A
In ΔRST
`∠ROT = 90° + 1/2 ∠S`
`∠ROT = 90° + 1/2 (x)`
`140° = 90° + 1/2 (x)`
`140° - 90° = 1/2 (x)`
Further solving for x, we get,
`50 = 1/2 (x)`
x = 2(50°)
x = 100°
Thus, x = 100°
APPEARS IN
RELATED QUESTIONS
Compute the value of x in the following figure:
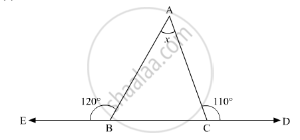
If two acute angles of a right triangle are equal, then each acute is equal to
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
Can a triangle together have the following angles?
55°, 55° and 80°
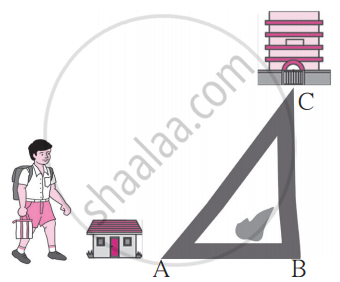
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
8.4 cm, 16.4 cm, 4.9 cm
Can you draw a triangle with 25°, 65° and 80° as angles?
In a ∆ABC, AB = AC. The value of x is ________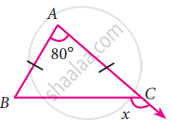
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
