Advertisements
Advertisements
Question
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
Solution
In the given problem, BP and CP are the internal bisectors of ∠B and ∠C respectively. Also, BQ and CQ are the external bisectors of ∠B and ∠C respectively. Here, we need to prove:
∠BPC +∠BQC = 180°
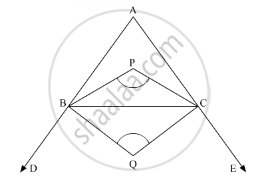
We know that if the bisectors of angles ∠ABC and ∠ACB of ΔABC meet at a point O then` ∠BOC = 90° + 1/2 ∠A`.
Thus, in ΔABC
`∠BPC = 90° + 1/2 ∠A.` ……(1)
Also, using the theorem, “if the sides AB and AC of a ΔABC are produced, and the external bisectors of ∠B and ∠Cmeet at O, then `∠BOC = 90° + 1/2 ∠A.` .
Thus, ΔABC
\[\angle BQC = 90^\circ - \frac{1}{2}\angle A . . . . . . \left( 2 \right)\]
Adding (1) and (2), we get
`∠BOC +∠BQC = 90° + 1/2 ∠A + 90° -1/2 ∠A`
∠BQC + ∠BQC = 180°
Thus, `∠BQC + ∠BQC = 180°
Hence proved.
APPEARS IN
RELATED QUESTIONS
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
Is the following statement true and false :
All the angles of a triangle can be equal to 60°.
Is the following statement true and false :
A triangle can have two obtuse angles.
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
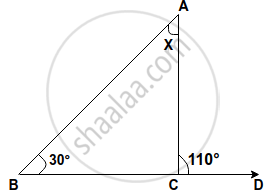
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
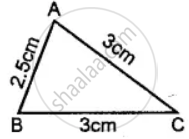
Classify the following triangle according to sides:
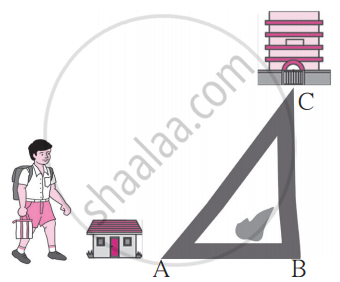
As shown in the figure, Avinash is standing near his house. He can choose from two roads to go to school. Which way is shorter? Explain why.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
8.4 cm, 16.4 cm, 4.9 cm
The angles of a triangle are in the ratio 2 : 3 : 4. Then the angles are
