Advertisements
Advertisements
Question
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
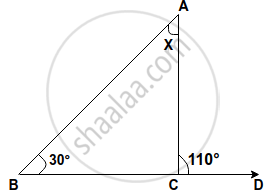
Solution
We know that,
Exterior angle of a triangle is always equal to the sum of its two interior opposite angles (property)
∴ 110° = x + 30° (by property)
⇒ x = 110°- 30°
x = 80°
APPEARS IN
RELATED QUESTIONS
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Can a triangle have two obtuse angles? Justify your answer in case.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

Is the following statement true and false :
A triangle can have two right angles.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
In ∆ABC, C = 56° C = 56° ∠B = ∠C and ∠A = 100° ; find ∠B.
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
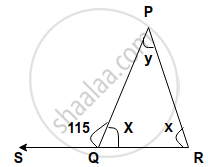
The length of the sides of the triangle is given. Say what types of triangles they are 4.3 cm, 4.3 cm, 4.3 cm.
Find all the three angles of the ΔABC
Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than `2/3` of a right angle.
