Advertisements
Advertisements
प्रश्न
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
उत्तर
In the given problem, BP and CP are the internal bisectors of ∠B and ∠C respectively. Also, BQ and CQ are the external bisectors of ∠B and ∠C respectively. Here, we need to prove:
∠BPC +∠BQC = 180°
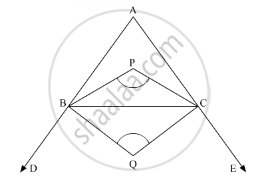
We know that if the bisectors of angles ∠ABC and ∠ACB of ΔABC meet at a point O then` ∠BOC = 90° + 1/2 ∠A`.
Thus, in ΔABC
`∠BPC = 90° + 1/2 ∠A.` ……(1)
Also, using the theorem, “if the sides AB and AC of a ΔABC are produced, and the external bisectors of ∠B and ∠Cmeet at O, then `∠BOC = 90° + 1/2 ∠A.` .
Thus, ΔABC
\[\angle BQC = 90^\circ - \frac{1}{2}\angle A . . . . . . \left( 2 \right)\]
Adding (1) and (2), we get
`∠BOC +∠BQC = 90° + 1/2 ∠A + 90° -1/2 ∠A`
∠BQC + ∠BQC = 180°
Thus, `∠BQC + ∠BQC = 180°
Hence proved.
APPEARS IN
संबंधित प्रश्न
Is the following statement true and false :
All the angles of a triangle can be less than 60°
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
State, if the triangle is possible with the following angles :
60°, 60°, and 50°
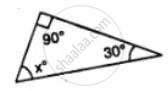
Calculate the unknown marked angles of the following figure :
Can a triangle together have the following angles?
85°, 95° and 22°
Classify the following triangle according to sides:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
17 cm, 7 cm, 8 cm
Can we have two acute angles whose sum is a reflex angle? Why or why not?
