Advertisements
Advertisements
प्रश्न
In a Δ ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q, Prove that ∠BPC + ∠BQC = 180°.
उत्तर
In the given problem, BP and CP are the internal bisectors of ∠B and ∠C respectively. Also, BQ and CQ are the external bisectors of ∠B and ∠C respectively. Here, we need to prove:
∠BPC +∠BQC = 180°
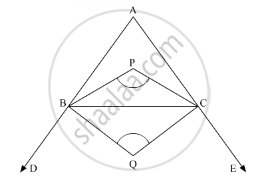
We know that if the bisectors of angles ∠ABC and ∠ACB of ΔABC meet at a point O then` ∠BOC = 90° + 1/2 ∠A`.
Thus, in ΔABC
`∠BPC = 90° + 1/2 ∠A.` ……(1)
Also, using the theorem, “if the sides AB and AC of a ΔABC are produced, and the external bisectors of ∠B and ∠Cmeet at O, then `∠BOC = 90° + 1/2 ∠A.` .
Thus, ΔABC
\[\angle BQC = 90^\circ - \frac{1}{2}\angle A . . . . . . \left( 2 \right)\]
Adding (1) and (2), we get
`∠BOC +∠BQC = 90° + 1/2 ∠A + 90° -1/2 ∠A`
∠BQC + ∠BQC = 180°
Thus, `∠BQC + ∠BQC = 180°
Hence proved.
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
Is the following statement true and false :
A triangle can have two right angles.
Is the following statement true and false :
An exterior angle of a triangle is greater than the opposite interior angles.
An exterior angle of a triangle is 108° and its interior opposite angles are in the ratio 4 : 5. The angles of the triangle are
State, if the triangle is possible with the following angles :
20°, 70°, and 90°
In the given figure, show that: ∠a = ∠b + ∠c
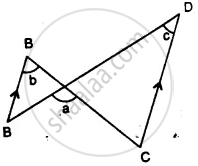
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
The length of the sides of the triangle is given. Say what types of triangles they are 3.7 cm, 3.4 cm, 4 cm.
Can 30°, 60° and 90° be the angles of a triangle?
Match the following:
| Column A | Column B |
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
What is common in the following figure?
 |
 |
| (i) | (ii) |
Is figure (i) that of triangle? if not, why?
