Advertisements
Advertisements
प्रश्न
In the given figure, show that: ∠a = ∠b + ∠c
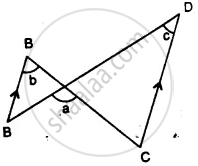
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
उत्तर
∵ AB || CD
∴ b = c and ∠A = ∠C ........(Alternate angles)
Now in Δ PCD,
Ext. ∠APC = ∠C + ∠D
⇒ a = b + c
(i) If b = 60°, c = 50°, then
a = b + c = 60° + 50° = 110°
(ii) If a = 100° and b = 55°,
then a = b + c
⇒ 100° = 55°+ c
⇒ c = 100°− 55° = 45°
(iii) If a = 108° and c = 48°
then a = b + c
⇒ 108° = b + 48°
⇒ b = 108°− 48° = 60°
APPEARS IN
संबंधित प्रश्न
Fill in the blank to make the following statement true:
A triangle cannot have more than ...... right angles.
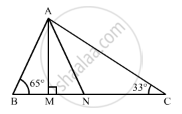
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
Classify the following triangle according to angle:
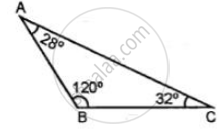
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
Can we have two acute angles whose sum is a right angle? Why or why not?
Can we have two acute angles whose sum is a straight angle? Why or why not?
