Advertisements
Advertisements
प्रश्न
In a triangle PQR, ∠P = 60° and ∠Q = ∠R, find ∠R.
उत्तर
Let ∠Q = ∠R = x, ∠P = 60°
But ∠P + ∠Q + ∠R = 180°
∴ 60° + x + x = 180°
⇒ 60° + 2x = 180°
⇒ 2x = 180° − 60° = 120°
⇒ x =`(120°)/2`=60°
∴ ∠Q = ∠R = 60°
Hence, ∠R = 60°
APPEARS IN
संबंधित प्रश्न
If the angles of a triangle are in the ratio 1: 2 : 3, determine three angles.
Can a triangle have two acute angles?Justify your answer in case.
AB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.

Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
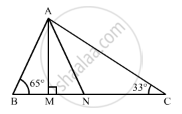
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
If the side BC of ΔABC is produced on both sides, then write the difference between the sum of the exterior angles so formed and ∠A.
Mark the correct alternative in each of the following:
If all the three angles of a triangle are equal, then each one of them is equal to
In the given figure, show that: ∠a = ∠b + ∠c
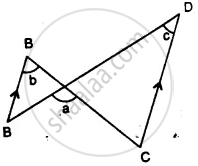
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
Can a triangle together have the following angles?
33°, 74° and 73°
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
