Advertisements
Advertisements
Question
One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
Solution
In Δ ABC,
Let ∠A = 61°
But ∠A + ∠B + ∠C = 180° ........(Angles of a triangle)
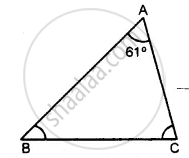
⇒ 61° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180°− 61° = 119°
But ∠B: ∠C =`1 1/2:1 1/3=3/2:4/3`
`=(9:8)/6`
=9: 8
Let ∠B = 9x and ∠C = 8x,
then, 9x + 8x = 119°
⇒ 17x = 119°
⇒ x =`(119°)/17=7°`
∴ ∠B = 9x = 9 × 7° = 63°
∠C = 8x = 8 × 7° = 56°
APPEARS IN
RELATED QUESTIONS
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
If two acute angles of a right triangle are equal, then each acute is equal to
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
Calculate the unknown marked angles of the following figure :
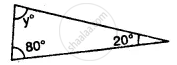
In the following, find the marked unknown angle:

Find, giving a reason, the unknown marked angles, in a triangle drawn below:

In the given figure, AB is parallel to CD. Then the value of b is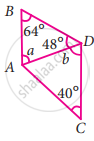
In ΔABC, name the 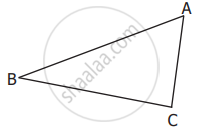
a) Three sides: _________, __________, __________
b) Three Angles: _________, __________, __________
c) Three Vertices: _________, __________, __________
Bisectors of the angles B and C of an isosceles triangle with AB = AC intersect each other at O. BO is produced to a point M. Prove that ∠MOC = ∠ABC.
Can we have two acute angles whose sum is an acute angle? Why or why not?
