Advertisements
Advertisements
प्रश्न
One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
उत्तर
In Δ ABC,
Let ∠A = 61°
But ∠A + ∠B + ∠C = 180° ........(Angles of a triangle)
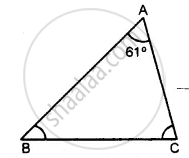
⇒ 61° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180°− 61° = 119°
But ∠B: ∠C =`1 1/2:1 1/3=3/2:4/3`
`=(9:8)/6`
=9: 8
Let ∠B = 9x and ∠C = 8x,
then, 9x + 8x = 119°
⇒ 17x = 119°
⇒ x =`(119°)/17=7°`
∴ ∠B = 9x = 9 × 7° = 63°
∠C = 8x = 8 × 7° = 56°
APPEARS IN
संबंधित प्रश्न
Can a triangle have All angles equal to 60°? Justify your answer in case.
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
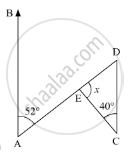
Compute the value of x in the following figure:
In a Δ ABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
Can a triangle together have the following angles?
55°, 55° and 80°
Find x, if the angles of a triangle is:
2x°, 4x°, 6x°
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.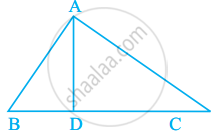
Can we have two acute angles whose sum is a right angle? Why or why not?
