Advertisements
Advertisements
Question
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
Solution
Given that the bisector of the exterior vertical angle of a triangle is parallel to the base and we have to prove that the triangle is isosceles
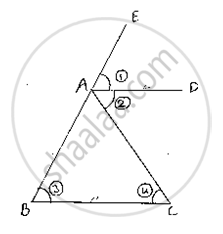
Let ABC be a triangle such that AD is the angular bisector of exterior vertical angle EAC and AD || BC
Let∠EAD = (1), ∠DAC = (2), ∠ABC = (3) and∠ACB = (4)
(1) = (2) [ ∵ AD is bisector of , ∠EAC ]
(1)=(3) [Corresponding angles]
and (2) = (4) [alternative angle]
⇒ (3) = (4) ⇒AB = AC
Since, in ΔABC, two sides AB and AC are equal we can say that
DABC is isosceles
APPEARS IN
RELATED QUESTIONS
The angles of a triangle are (x − 40)°, (x − 20)° and `(1/2x-10)^@.` find the value of x
The angles of a triangle are arranged in ascending order of magnitude. If the difference
between two consecutive angles is 10°, find the three angles.
Can a triangle have two right angles? Justify your answer in case.
In the given figure, AB || DE. Find ∠ACD.

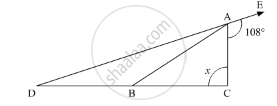
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
7 cm, 24 cm, 25 cm
The angles of a triangle are in the ratio 2 : 3 : 4. Then the angles are
In the given figure, AB is parallel to CD. Then the value of b is