Advertisements
Advertisements
प्रश्न
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosce
उत्तर
Given that the bisector of the exterior vertical angle of a triangle is parallel to the base and we have to prove that the triangle is isosceles
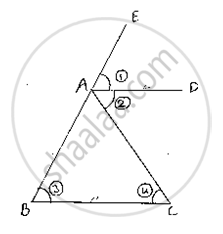
Let ABC be a triangle such that AD is the angular bisector of exterior vertical angle EAC and AD || BC
Let∠EAD = (1), ∠DAC = (2), ∠ABC = (3) and∠ACB = (4)
(1) = (2) [ ∵ AD is bisector of , ∠EAC ]
(1)=(3) [Corresponding angles]
and (2) = (4) [alternative angle]
⇒ (3) = (4) ⇒AB = AC
Since, in ΔABC, two sides AB and AC are equal we can say that
DABC is isosceles
APPEARS IN
संबंधित प्रश्न
ABC is a triangle in which ∠A — 72°, the internal bisectors of angles B and C meet in O.
Find the magnitude of ∠BOC.
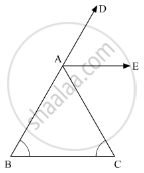
In the given figure, AE bisects ∠CAD and ∠B= ∠C. Prove that AE || BC.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
Can a triangle together have the following angles?
55°, 55° and 80°
Find x, if the angles of a triangle is:
2x°, 4x°, 6x°
In ∆ABC, ∠A = ∠B = 62° ; find ∠C.
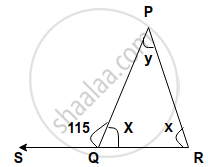
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
Classify the following triangle according to sides:
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
In figure, AB = BC and AD = BD = DC. The number of isosceles triangles in the figure is ______.