Advertisements
Advertisements
प्रश्न
An exterior angle of a triangle is equal to 100° and two interior opposite angles are equal. Each of these angles is equal to
पर्याय
75°
80°
80°
40°
50°
उत्तर
n the ΔABC, CD is the ray extended from the vertex C of ΔABC. It is given that the exterior angle of the triangle is 100° and two of the interior opposite angles are equal.
So, ∠ACD = 100° and A = ∠B
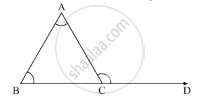
So, now using the property, “an exterior angle of the triangle is equal to the sum of the two opposite interior angles”, we get.
In ΔABC
∠A + ∠B = ∠ACD
∠2A = 100°
`∠A = (100°)/2`
∠A = 50°
∠A = ∠B = 50°
Therefore, each of the two opposite interior angles is 50°.
APPEARS IN
संबंधित प्रश्न
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
The exterior angles, obtained on producing the base of a triangle both way are 104° and 136°. Find all the angles of the triangle.
In ΔPQR, If ∠R > ∠Q then ______.
If the angles of a triangle are equal, find its angles.
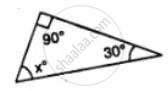
Find the unknown marked angles in the given figure:
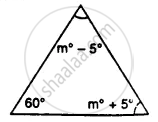
Calculate the unknown marked angles of the following figure :
One of the base angles of an isosceles triangle is 52°. Find its angle of the vertex.
In the following, find the marked unknown angle:
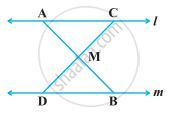
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
The number of triangles in figure is ______. Their names are ______.