Advertisements
Advertisements
प्रश्न
Two angles of a triangle are equal and the third angle is greater than each of those angles
by 30°. Determine all the angles of the triangle.
उत्तर
Given that,
Two angles are equal and the third angle is greater than each of those angles `by 30^@` Let x, x, x+30 be the angles of a triangle
We know that
Sum of all angles of a triangle is `180^@`
`x+x+x+30=180^@`
`3x+30=180^@`
`3x=180^@-30^@`
`3x=150^@`
`x=150^@/3`
`x=50^@`
∴ The angles are x,x,x+30
`x=50^@`
`x+30=80^@`
∴ The required angles are `50^@,50^@, 80^@`
APPEARS IN
संबंधित प्रश्न
Compute the value of x in the following figure:
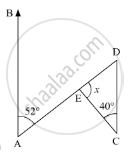
Is the following statement true and false :
A triangle can have two obtuse angles.
Fill in the blank to make the following statement true:
An exterior angle of a triangle is equal to the two ....... opposite angles.
In the given figure, compute the value of x.
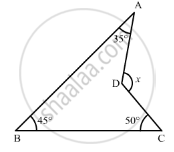
In Δ ABC, if u∠B = 60°, ∠C = 80° and the bisectors of angles ∠ABC and ∠ACB meet at a point O, then find the measure of ∠BOC.
If two acute angles of a right triangle are equal, then each acute is equal to
In the following, find the marked unknown angle:

Can a triangle together have the following angles?
55°, 55° and 80°
One angle of a right-angled triangle is 70°. Find the other acute angle.
One of the angles of a triangle is 65°. If the difference of the other two angles is 45°, then the two angles are
