Advertisements
Advertisements
प्रश्न
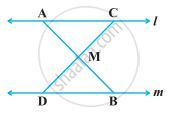
In the following figure, l || m and M is the mid-point of a line segment AB. Show that M is also the mid-point of any line segment CD, having its end points on l and m, respectively.
उत्तर
Given: In the following figure, l || m and M is the mid-point of a line segment AB i.e., AM = BM.
To show: MC = MD
Proof: l || m ...[Given]
∠BAC = ∠ABD ...[Alternate interior angles]
∠AMC = ∠BMD ...[Vertically opposite angles]
In ΔAMC and ΔBMD,
∠BAC = ∠ABD ...[Proved above]
AM = BM ...[Given]
And ∠AMC = ∠BMD ...[Proved above]
∴ ΔAMC ≅ ΔBMD ...[By ASA congruence rule]
⇒ MC = MD ...[By CPCT]
APPEARS IN
संबंधित प्रश्न
The angles of a triangle are arranged in ascending order of magnitude. If the difference
between two consecutive angles is 10°, find the three angles.
The bisectors of base angles of a triangle cannot enclose a right angle in any case.
Can a triangle have All angles more than 60°? Justify your answer in case.
Side BC of a triangle ABC has been produced to a point D such that ∠ACD = 120°. If ∠B = \[\frac{1}{2}\]∠A is equal to
Find the unknown marked angles in the given figure:
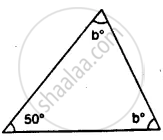
Find the unknown marked angles in the given figure:
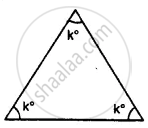
In the following, find the marked unknown angle:

Can a triangle together have the following angles?
85°, 95° and 22°
Classify the following triangle according to sides:
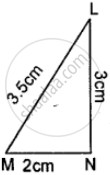
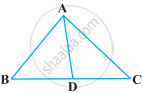
In the following figure, AD is the bisector of ∠BAC. Prove that AB > BD.